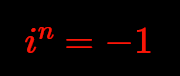
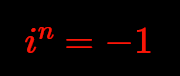
Atomic vector subspaces are those vector subspaces, which are isomorphic to the complex plane $\mathbb C$ or to the real line $\color{blue}{\mathbb R}$ and their multiplicative identity has the length of $\sqrt {d_k \over n}$ in the vector space. Hereby is $d_k$ the dimensional count of the k-th atomic vector subspace, and its value is: $d_k=\cases {\color{blue}{1: \space \forall k= {n-1 \over 2}} \\ 2: \space \forall k<{n-1 \over 2}} $. According to this dimension count we can call them complex atoms or the (remaining) real atom.

The real atomic unit vector (with name r) will always satisfy: $\hat r_k^2 = \hat r_k$, and their j-th coordinate is:

$(\hat r_k)_j={d_k \over n}\cdot \cos \left( {(2k+1)\cdot j \over n} \cdot π \right)$.

The imaginary atomic unit (with name i) will always satisfy: $\hat i_k^2 = -\hat r_k$, and their j-th coordinate is:

$(\hat i_k)_j={2 \over n}\cdot \sin \left( {(2k+1)\cdot j \over n} \cdot π \right)$.

Actually the additive inverse of the imaginary unit would satisfy all requirements, I just followed the convetion from the complex numbers and associated i with plus sine, instead of the minus of sine.

The product of unit vectors of different atoms will always be zero: $\forall j \ne k: \space \hat r_j \cdot \hat r_k = \hat r_j \cdot \hat i_k = \hat i_j \cdot \hat i_k = 0$.

The sum off all real atomic units is the real unit of the vector space: $\sum \hat r_k = 1$.

For n=1 and n=2 the atomic unit vectors are identical with the unit vectors of the vector space.

All atomic unitvectors together are the atomic basis, an orthogonal basis for the vector space: $A_n=(\hat r_0, \hat i_0, \hat r_1, \hat i_1, \ldots )$.
If we transform $\vec x$ onto the atomic base: $\vec x' = A_{n= {\color{blue}{1+}}2k }^{-1} \cdot \vec x$ and its multiplication matrix:

$M'_{n= {\color{blue}{1+}}2k } = A_n^{-1} \cdot M_n \cdot A_n=\begin{pmatrix} x'_0 & -x'_1 & 0 & 0 & 0 & 0 & \cdots & {\color{blue} 0} \\ x'_1 & x'_0 & 0 & 0 & 0 & 0 & \cdots & {\color{blue} 0} \\ 0 & 0 & x'_2 & -x'_3 & 0 & 0 & \cdots & {\color{blue} 0} \\ 0 & 0 & x'_3 & x'_2 & 0 & 0 & \cdots & {\color{blue} 0} \\ 0 & 0 & 0 & 0 & x'_4 & -x'_5 & \cdots & {\color{blue} 0} \\ 0 & 0 & 0 & 0 & x'_5 & x'_4 & \cdots & {\color{blue} 0} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & {\color{blue} \vdots} \\ \color{blue} 0 & \color{blue} 0 & \color{blue} 0 & \color{blue} 0 & \color{blue} 0 & \color{blue} 0 & \color{blue} \cdots & \color{blue} x'_{n-1} \end{pmatrix}$

then we reduce the massive calculations of the n-dimensional vector multiplication to a minimum of complex multiplications, in case of odd-dimensional vector spaces with one additional real multiplication.

Beside of the definition and some basic properties of the vector multiplication, all main statements are on this page. All other regularities described in zero divisors and on the coming pages are more or less trivial conclusions from this page. Even the transformed multiplication matrix is equivalent to the splitted statements about the atomic units.

But before we prove them, I would like to present one more argument to call them atoms...